No Dice No Problem (0D0P)
A downloadable game
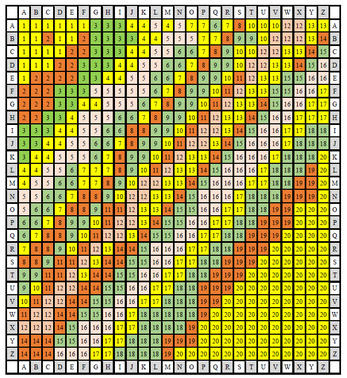
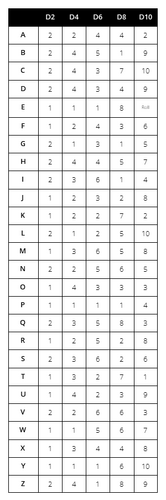
The No Dice No Problem (0D0P) bookmark allows you to play truly diceless games, "rolling" random results from D2, D4, D6, D8, D10, or D20 by using the nearest book, magazine, online article, or any writing you may have near by!
Numbers are assigned to letters based on the frequency of their use in English. While each number may not appear as frequently on the table, they are tied to letters that are seen at a frequency totaling near what one should see when rolling the die.
0D0P is the engine behind A Novel Dungeon, a completely diceless dungeon delving system that generates a dungeon based on a novel's title and encounters on its contents.
0D0P is available for use under the Creatives Commons Attribution (CC-BY) license using the Attribution Text below:
This work includes the No Dice No Problem (0D0P) system (found at https://serialprizes.itch.io/0d0p), a product of Jason Kenney and Serial Prizes, and licensed for our use under the Creative Commons Attribution 3.0 Unported license (https://creativecommons.org/licenses/by/3.0/).
If you use the 0D0P system, please let us know in the comments so we can link to your creation! Thanks.
| Status | Released |
| Category | Physical game |
| Rating | Rated 4.8 out of 5 stars (12 total ratings) |
| Author | Serial Prizes |
| Genre | Role Playing |
| Tags | bookmark, Dice, diceless, Supplement, Tabletop |
Download
Click download now to get access to the following files:
Development log
- Design tweak and DOCX available!Nov 15, 2023
- Roll a D20 with just a book!Nov 14, 2023
- 0d0p UPDATEDNov 06, 2023
- 0d0p in the wildSep 25, 2023
- D2-D10 All-in-oneOct 26, 2022
- Now “roll” a D10!Oct 26, 2022

Comments
Log in with itch.io to leave a comment.
This is neat! I did something adjacent with a bookmark that generates 1d6 or 2d6 results based on English letter frequency a while back. It's interesting for me to see someone else using the same data with the same intent produce such a different end product.
This is a very clever system!
Thanks!
The current pip distribution suggests (sums) the probability for D10 (in two columns):
result | probability (%)
9 | 14,8
6 | 2,8
If letter R would be coded to 6 instead of 9, the probability for the two would change to
9 | 8,8
6 | 8,8
Is the source code open and where is it located, please? I see that you are probably using gSheet/gDoc to generate the optimal distribution. I would like to create a similar table for Czech language employing the statistical distribution for the Czech alphabet.
I admire you to go for gDocs. I cannot see myself building the algorithm in any spreadsheet -- simply due to the assumed algorithmical complexity) -- I would rather aim for a Python script.
So it's not actually code or algorithm driven -- it's a manual process based off of research others have done on letter frequency and then I pick a roughly even number of letters to get to comparable odds of a die roll.
For Czech I found a letter frequency chart here and using that I generated the following chart:
Please let me know if that works or if something is off frequency wise, but if it's good I'd be happy to churn out a Czech translation of the final doc.
Thank you for the prompt answer. The referenced source is a private research and requires proper referencing when used. Instead, I would suggest to go with the frequencies listed on the Wikipedia. Use the frequency values for joint groups (a+á, c+č).
What? Manually?! Good job! My script for generating the D4 column is still running. Several hours over night…
(Curiosity engaged: did you later find a bug that drove up the runtime? Is your script on GitHub or similar?)
Bugs fixed. Code improved. Doc is missing. In progress.
https://github.com/kofaysi/0d0p
Cool, glad to hear you fixed it!
Would it be possible to have a bookmark that had a d10 on it? Or does the math not work out? I would make more use of a d10 than a d2.
Unfortunately it wouldn't be entirely accurate as a d10 to spread across all possible outcomes since the instance rate of E alone is 12% (see below).
But, if you have a system that measures success/fail over a specific number then you could average it out overall -- in a 6-or-better instance spread 50% across 1-5, the other 50% across 6-10.
Quick version below. You could break this into numbers but E will always throw it off.
I wonder if you could tweak it such that E was roll again. Thanks for the data and the detailed response!
Not a bad suggestion for a "roll again." Gets you closer to a d10, though instance of T is just over 10% if E is taken out of the equation. But it's MUCH closer (see below).
And happy to help - I've been mulling over a d10 for a while so thank YOU for the "roll again" suggestion. Looking better.
Wow! That's definitely close enough for casual use. The T rounds down to 10%, at least.
Ship it? :)
Done! Listing updated with a new bookmark. Thanks!